Konsep Dasar Kriptografi part 3 Cryptanalysis part 1 Known plaintext Attack
Cryptanalysis
Cryptanalysis adalah teknik untuk mencoba memecahkan enkripsi, biasanya dengan cara mencari kunci enkripsi. Ada 3 ketegori teknik pencarian kunci yang biasanya digunakan pada kriptografi klasik :
1) known plaintext attack
2) analisa statistik
3) brute force search
Algoritma enkripsi klasik yang baik adalah algoritma yang tahan terhadap known plaintext attack dan analisa statistika sehingga pencari kunci harus dilakukan dengan brute force search. Tentu saja kunci enkripsi harus lah besar agar tidak mudah ditebak dan menjadikan brute force search tidak efektif karena membutuhkan waktu yang lama biasa nya.
Berbeda dengan kriptografi klasik, kriptografi public key mengandalkan keamanannya pada sukarnya komputasi untuk mendapatkan kunci rahasia, yaitu :
1) penguraian bilangan bulat yang besar 2) komputasi algoritma diskrit untuk finite field yang besar
Jadi pemecahan kunci untuk kriptografi public key difokuskan pada teknik-teknik untuk mempercepat kedua komputasi tersebut.
Pada Konsep Dasar Kriptografi part 2 Cryptanalysis part 1 bagian ini saya akan membahas Known Plaintext Attact. Pada part selanjut akan dibahas satu persatu.
• Known plaintext Attack
Known plaintext attack adalah teknik pencarian kunci enkripsi berdasarkan pengetahuan mengenai pasangan asli – naskah acak. Kita akan menggunakan Ceaser chiper sebagai contoh dari enkripsi yang rentan terhadap known plaintext attack.
Julius caesar menukar setiap huruf dalam naskah asli dengan huruf lain dalam naskah acak. Besar atau kecil huruf dipertahankan dalam naskah acak (huruf besar ditukar dengan huruf besar, huruf kecil ditukar dengan huruf kecil), spasi, titik, koma dan tanda lainnya tidak ditukar.
Ceaser cipher adalah jenis enkripsi yang disebut simple substitution chiper dimana setiap huruf dalam naskah asli ditukar dengan huruf lain dalam naskah acak.
Julius Caesear menukar huruf dengan cara shift transformation. Rumus umum untuk shift transformation adalah :
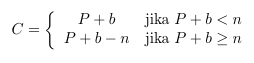
dimana :
C adalah kode bilangan karakter acak,
P adalah kode bilangan karakter asli,
b adalah bersarnya shift,
n adalah besarnya perbendaharaan karakter (dengan kode 0 sampai n – 1).
jadi rumus untuk enkripsi sesuai dengan relasi ekuivalen:
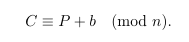
Rumus untuk dekripsi juga sesuai dengan relasi ekuivalen gambar diatas.
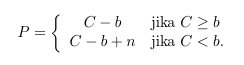
Julius Caesar sendiri menggunakan huruf “A” sampai “Z” (dengan code 0 sampai 25) sebagai perbendaharaan karakter untuk enkripsi (karakter selain huruf tidak dienkripsi), dan menggunakan parameter b = 3 menghasilkan rumus enkripsi.
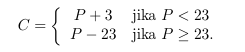
Jadi untuk enkripsi, 0 (“A”) ditukar dengan 3 (“D”), 1 (“B”) dengan 4 (“E”), …. , 24 (“Y”) dengan 1 (“B”), dan 25 (“Z”) dengan 2 (“C”).
Rumus dekripsi menjadi
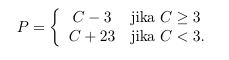
| Keterangan | Nilai/isi dari naskah |
|---|---|
| Naskah Asli | Jangan rahasiakan pesan ini! |
| Naskah Setelah Di Acak | Mdqjdq udkdvldndq shvdq lql! |
Tingkat kesukaran known-plaintext attack tergantung pada rumus yang digunakan untuk enkripsi. Semakin rumit rumus yang digunakan, semakin sukar untuk melakukan known-plaintext attack. Rumus yang bersifat linear masih tergolong sederhana dan dianggap rentan terhadap known-plaintext attack. Semakin non-linear dan semakin banyak parameter yang digunakan untuk rumus, semakin sulit untuk mengkalkulasi kunci berdasarkan rumus.
sumber : Teori dan Aplikasi Kriptografi
Penulis: Sentot Kromodimoeljo
Januari 2010
Let me know what you think of this article in the comment section below!